tugas 1 blog mata kuliah aljabar linear

Nama                   : Alfian Riswandi

NIM                     : 202231005

Kelas                    : A

Fakultas               : Telematika Energi

Program Studi    : S1 Teknik Informatika

Mata Kuliah        : Aljabar Linear

A Pengertian Matrik

Matriks adalah susunan bilangan real yang berbentuk empat persegi panjang dan di batasi oelh tanda kurung. Pemberian nama elemen disesuaikandengan letak baris dan kolomnya. Bagian yang mendatar ( horizontal ) disebut dengan baris. Sedangkan bagian yang tegak ( vertikal ) disebut dengan kolom. Matrik dengan jumlah baris = m, jumlah kolom = n disebut dengan ukuran (mxn) atau matrik berordo (mxn)


Jenis-Jenis Matrik

a.    Matrik Segitiga Atas

 A dikatakan matrik segitiga atas, jika A adalah matrik bujur sangakar dimana semua elemen dibawah / diatas diagonal utama 0



Elemen-elemen diagonal utama : 3,9,-7,2,8 elemen-elemen di bawah ini diagonal utama 0, maka A matrik segitiga atas





Elemen-elemen diagonal utama : 1,4,7,2,8 elemen-elemen di atas diagonal utama 0, maka A matrik segitiga bawah

b.Matrik Bujur Sangkar

A dikatakan matrik bujur sangkar jika jumlah baris dan jumlah kolom sama. Matrik A dikatakan berordo (n).


Elemen-elemen diagonal utama A adalah a11,a22,a33,a44,…..

    Contoh :

 Matrik A berordo 4, elemen-elemen diagonal utama A

c.Mantrik Diagonal

A dikatakan matrik diagonal, jika A adalah matrik bujur sangkar dimana semua elemen selain diagonal utama 0, dan elemen diagonal utama tak nol. Matrik demikian diberi lambang D.


d.Matrik Identitas

A dikatakan matrik identitas, jika A adalah matrik bujur sangkar dimana semua elemen selain diagonal utama 0, dan elemen diagonal utama 1. Matrik identitas diberi lambang I.



e.  Matrik Baris
Matrik baris adalah matrik yang terdiri dari saty baris

Contoh : A = ( 1 3 4 9 )

f. Matriks Kolom
Matrik kolom adalah matriks yang terdiri dari satu kolom
Contoh :
                                                

g. Matrik Nol
Matriks nol adalah suatu matriks yang setiap unsurnya 0 berordo, ditulis dengan huruf O.

h. Matrik Skalar
Matriks skalar adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya sama.



i.Transpose Matriks

Transpose matrik A ditulis AT adalah sebuah matrik yang diperoleh dari A dimana baris AT adalah kolom A, dan kolom AT adalah baris A. Bila A berukuran (mxn), AT berukuran (nxm).



j. Matrik Simetris

A dikatakan matrik simetris bilamana A adalah matrik bujur sangkar dimana, AT = A.



k. Matriks Mendatar

Matrik mendatar adalah matrik yang banyaknya baris kurang dari banyaknya kolom.



l. Matriks Tegak

Matriks tegak adalah suatu matriks yang banyaknya kolom lebih dari banyaknya baris.




m. Matriks Skew Simetris (Anti Simetri)

Yaitu suatu matriks persegi yang apabila ditransposkan akan sama dengan negative dari matriks semula. Misalkan A adalah matriks persegi. Matriks A dikatakan skew simetris jika dan hanya jika AT = -A. Syarat tandanya yaitu semua elemen yang berada di diagonal utama bernilai nol.



Operasi Aritmatika Matrik

a. Sifat Penjumlahan Matrik

Misalkan terdapat matriks A,B,C dan matriks nol O demikian sehingga berlaku :

A+B = B+A

A+(B+C) = (A+B)+C

A+O = O+A = A

A+(-A) = -A+A = O

b. Sifat Perkalian Matrik

Misalkan terdapat matriks A,B,C, matrik nol O, matrik identitas I dan m,n sembarang bilangan bulat yang sedemikan rupa sehingga berlaku :

1.    Assosiatif   : (AB)C = A(BC) 

2.    Distribusi kiri : A(B+C) = AB+AC

3.    Distribusi kanan : (B+C)A = BA+CA

4.    Sifat perkalian dengan konstanta : k (AB) = (kA)B = A (Kb), dimana k konstanta real

5.    Sifat perkalian dengan matriks satuan : AI = IA = A


c.Kesamaan, A = B

Matrik, A = [ajj] dan B[bjj] dikatakan sama ditulis A = B jika

1)    A dan B berukuran sama

2)    Setiap elemen yang seletak nilai sama, ajj = ajj;


A dan B berukuran sama (2x3) tetapi A B, karena terdapat seletak nilainya tidak sama

d.Perkalian dengan scalar, kA

Perkalian matrik, A = [ajj] dengan scalar tak nol k ditulis kA, didefinisikan bahwa setiap elemen A dikalikan dengan konstanta tak nol k, yakni :
















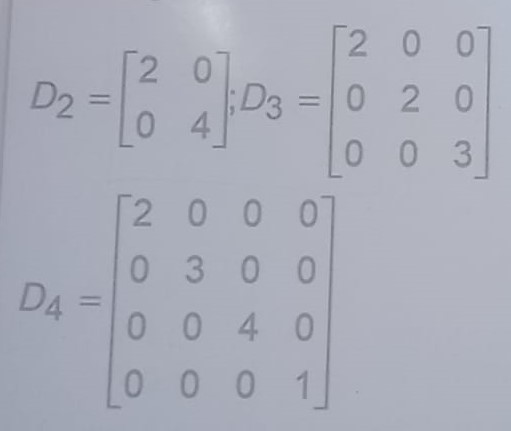
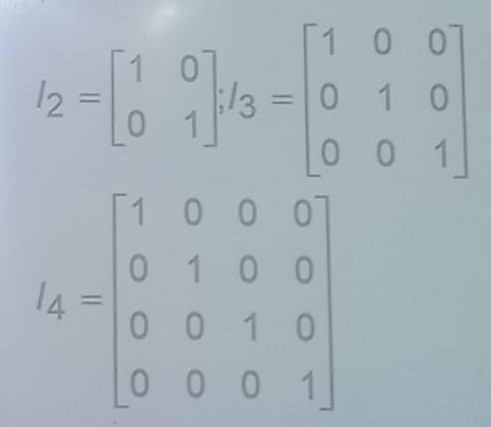
Komentar

Posting Komentar

Postingan populer dari blog ini

Sejarah & Perkembangan Prosesor AMD

Gambar
SEJARA DAN PERKEMBANG PROSESOR AMD Sejarah perusahaan ini dimulai pada tahun 1969 di Sunnyvale, California. Perusahaan ini didirikan oleh Jerry Sanders dan sekelompok insinyur dari Fairchild Semiconductor. Sejak itu, AMD terus mengembangkan prosesor yang inovatif dan berkualitas tinggi. Pada awalnya, AMD hanya menjadi pemasok komponen elektronik untuk perusahaan lain. Namun, pada tahun 1975, AMD memutuskan untuk membuat prosesor mereka sendiri dengan peluncuran perdana prosesor AMD, yakni AMD Am9080. Prosesor ini adalah prosesor 8-bit yang dirancang untuk digunakan pada mesin-mesin industri. Namun, prosesor ini tidak begitu sukses dan AMD kemudian beralih ke pasar prosesor mikro. Pada tahun 1982, AMD meluncurkan prosesor 16-bit pertamanya, AMD Am29116. Prosesor ini dirancang untuk digunakan pada sistem komputer desktop dan berhasil menjadi saingan kuat bagi Intel. Namun, AMD baru benar-benar populer pada tahun 1991 dengan peluncuran prosesor 386DX, yang diluncurkan sebagai alternatif y
Baca selengkapnya

Tugas Blog Mikroprocessor

Gambar
  ARDUINO  Arduino  adalah pengendali mikro dengan papan tunggal yang berfungsi dalam proyek perangkat lunak sumber terbuka. Fungsi utama dari Arduino untuk memudahkan penggunaan elektronik dalam berbagai bidang. Arduino memiliki perangkat lunak yang menggunakan prosesor Atmel AVR. Sementara perangkat lunak yang dimiliki oleh Arduino terdiri dari beberapa alat yakni lingkungan pengembagan terpadu(IDE), penyunting teks,kompilator, Serial Monitor, dan Serial ISP Programer. Arduino juga merupakan senarai perangkat keras terbuka yang ditujukan kepada siapa saja yang ingin membuat purwarupa peralatan elektronik interaktif berdasarkan hardware dan software yang fleksibel dan mudah digunakan. Pada aplikasi Arduino, Mikrokontroler diprogram menggunakan bahasa pemograman C atau C++, dengan pustaka khas arduino. Karena sifatnya yang terbuka maka siapa saja dapat mengunduh skema hardware arduino dan membangunnya. Arduino menggunakan keluarga pengendali mikro ATMega yang dirilis oleh Atmel sebagai
Baca selengkapnya

Tugas 9 blog mata kuliah aljabar linear

Gambar
  Nama                    : Alfian Riswandi NIM                      : 202231005 Kelas                    : A Fakultas               : Telematika Energi Program Studi     : S1 Teknik Informatika Mata Kuliah        : Aljabar Linear BASIS DAN DIMENSI Ruang -N Euclides Jika n sebuah bilangan bulat positif, maka n-pasangan bilangan berturut adalah sebuah urutan n bilangan real ( x 1 , x 2 , ..., x n ). Himpunan semua n pasangan bilangan berurutan dinamakan ruang n Eucides dan dinyatakan dengan R n . RUANG VEKTOR Misalkan V sembarang himpunan. V dikatakan sebagai ruang vektor bilamana aksioma-aksioma berikut dipenuhi : 1. Jika u dan v vektor-vektor di V, maka u + v juga berada di V 2. u + v = v +u 3. u + (v + w) = (u + v) + w 4. Ada sebuah vektor 0 di V sehingga 0 + u = u + 0 5. Untuk setiap u di V terdapat -u di V sehingga u + (-u) = -u + u = 0 6. Jika k scalar dan u di V, maka ku berada di V 7. k(u + v) = ku + kv . (k + I) u = ku + Iu 9. k(u) = (kI) u 10. 1
Baca selengkapnya