Tugas 7 blog mata kuliah aljabar linear

 Nama                   : Alfian Riswandi

NIM                     : 202231005

Kelas                    : A

Fakultas               : Telematika Energi

Program Studi    : S1 Teknik Informatika

Mata Kuliah        : Aljabar Linear

NILAI EGIEN DAN VEKTOR EIGEN

Andaikan A marik bujur sangkar berordo nxn, vektor taknol x di dalam Rn dikatakan vektor eigen A, jika tedapat skalar taknol l sedemikian rupa sehingga,

Ax = lx

l disebut dengan nilai eigen dari A dan x disebut vektor eigen dari A yang bersesuaian dengan l.

Contoh :

Vektor x = [1,2] adalah vektor eigen dari :

 

yang bersesuaian dengan nilai eigen, l = 3, karena : 

Teknik Menghitung Nilai Eigen

Untuk menghitung nilai eigen matrik A yang berordo n x n tulislah Ax =  lx sebagai 

Ax = l|x

(l| - A)X = 0

Agar supaya  menjadi nilai eigen, maka penyelesaian system persamaan linear diatas non trivial, dimana syaratnya adalah:

ln + C1ln-1 + … + Cn - 1l + Cn = 0

Teknik Menghitung Nilai Eigen (2)

Persamaan terakhir adalah polinomial l berderajad n yang disebut dengan persamaan karakteristik A, sedangkan nilai eigen matrik A adalah akar-akar persamaan karakteristik A (akar-akar polinomial dalam l).

Langkah – Langkah menentukan nilai eigen dan vector eigen matrik A adalah :

1. Bentuk matrik (l| - A)

2. Hitung determinan, det(l| - A) = 0

3. Tentukan persamaan karakteristik dari , (l| - A) = 0

4. Hitung akar-akar persamaan karakteristik (nilai lamda)

5. Hitung vector eigen dari SPL, (l| - A) x = 0

Contoh

Carilah nilai eigen dan vector eigen dari,


Jawab

Bentuk, l| - A yaitu :

Persamaan karakteristiknya adalah :

det(l| - A) = l2 - 2l - 8 = 0

Akar – akar persamaan karekteristiknya adalah : l1 = 4, dan l2 = -2, dan inilah nilai eigen matrik A.

Vektor eigen x dari A diperoleh dari :

Untuk l = 4, diperoleh SPL

Solusi SPL diatas adalah :

jadi vector eigen untuk l = 4, adalah x = [5,1]. Sedangkan vector eigen yang bersesuaian dengan l = -2 adalah, x = [1,1].

Contoh

Carilah nilai eigen dan vector eigen dari,



 Jawab

Bentuk, l| - A yaitu:

Persamaan karakteristiknya adalah :

det(l| - A) = l3 - 6l2 + 11l - 6 = 0

Akar – akar persamaan karakteristiknya adalah : l1 = 1, l2 = 2, dan l3 = 3

Vektor eigen x dari A diperoleh dari :

Untuk l = 1, diperoleh SPL

Solusi SPL diatas adalah :


Jadi vector eigen yang bersesuaian dengan : 


























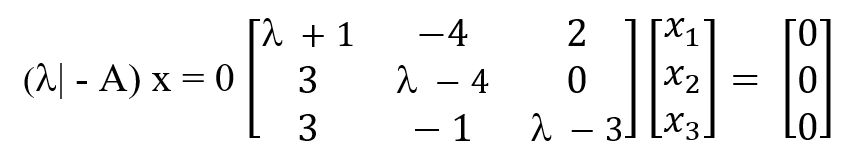
Komentar

Posting Komentar

Postingan populer dari blog ini

Sejarah & Perkembangan Prosesor AMD

Gambar
SEJARA DAN PERKEMBANG PROSESOR AMD Sejarah perusahaan ini dimulai pada tahun 1969 di Sunnyvale, California. Perusahaan ini didirikan oleh Jerry Sanders dan sekelompok insinyur dari Fairchild Semiconductor. Sejak itu, AMD terus mengembangkan prosesor yang inovatif dan berkualitas tinggi. Pada awalnya, AMD hanya menjadi pemasok komponen elektronik untuk perusahaan lain. Namun, pada tahun 1975, AMD memutuskan untuk membuat prosesor mereka sendiri dengan peluncuran perdana prosesor AMD, yakni AMD Am9080. Prosesor ini adalah prosesor 8-bit yang dirancang untuk digunakan pada mesin-mesin industri. Namun, prosesor ini tidak begitu sukses dan AMD kemudian beralih ke pasar prosesor mikro. Pada tahun 1982, AMD meluncurkan prosesor 16-bit pertamanya, AMD Am29116. Prosesor ini dirancang untuk digunakan pada sistem komputer desktop dan berhasil menjadi saingan kuat bagi Intel. Namun, AMD baru benar-benar populer pada tahun 1991 dengan peluncuran prosesor 386DX, yang diluncurkan sebagai alternatif y
Baca selengkapnya

Tugas Blog Mikroprocessor

Gambar
  ARDUINO  Arduino  adalah pengendali mikro dengan papan tunggal yang berfungsi dalam proyek perangkat lunak sumber terbuka. Fungsi utama dari Arduino untuk memudahkan penggunaan elektronik dalam berbagai bidang. Arduino memiliki perangkat lunak yang menggunakan prosesor Atmel AVR. Sementara perangkat lunak yang dimiliki oleh Arduino terdiri dari beberapa alat yakni lingkungan pengembagan terpadu(IDE), penyunting teks,kompilator, Serial Monitor, dan Serial ISP Programer. Arduino juga merupakan senarai perangkat keras terbuka yang ditujukan kepada siapa saja yang ingin membuat purwarupa peralatan elektronik interaktif berdasarkan hardware dan software yang fleksibel dan mudah digunakan. Pada aplikasi Arduino, Mikrokontroler diprogram menggunakan bahasa pemograman C atau C++, dengan pustaka khas arduino. Karena sifatnya yang terbuka maka siapa saja dapat mengunduh skema hardware arduino dan membangunnya. Arduino menggunakan keluarga pengendali mikro ATMega yang dirilis oleh Atmel sebagai
Baca selengkapnya

Tugas 9 blog mata kuliah aljabar linear

Gambar
  Nama                    : Alfian Riswandi NIM                      : 202231005 Kelas                    : A Fakultas               : Telematika Energi Program Studi     : S1 Teknik Informatika Mata Kuliah        : Aljabar Linear BASIS DAN DIMENSI Ruang -N Euclides Jika n sebuah bilangan bulat positif, maka n-pasangan bilangan berturut adalah sebuah urutan n bilangan real ( x 1 , x 2 , ..., x n ). Himpunan semua n pasangan bilangan berurutan dinamakan ruang n Eucides dan dinyatakan dengan R n . RUANG VEKTOR Misalkan V sembarang himpunan. V dikatakan sebagai ruang vektor bilamana aksioma-aksioma berikut dipenuhi : 1. Jika u dan v vektor-vektor di V, maka u + v juga berada di V 2. u + v = v +u 3. u + (v + w) = (u + v) + w 4. Ada sebuah vektor 0 di V sehingga 0 + u = u + 0 5. Untuk setiap u di V terdapat -u di V sehingga u + (-u) = -u + u = 0 6. Jika k scalar dan u di V, maka ku berada di V 7. k(u + v) = ku + kv . (k + I) u = ku + Iu 9. k(u) = (kI) u 10. 1
Baca selengkapnya